Review session on Wednesday 10/11 from 7-9 pm in Lawerence 115

Why do proteins fold?

2017-10-06

Conceptual goals

• Understand that folding is a tight balance between enthalpic and entropic terms

Skill goals

• Manipulate thermodynamic equations describing protein stability to calculate contributions of different forces
• Reason correctly about interactions by thinking correctly about both sides of a reaction coordinate

$$U \rightleftarrows F$$

• What changes between $U$ and $F$?

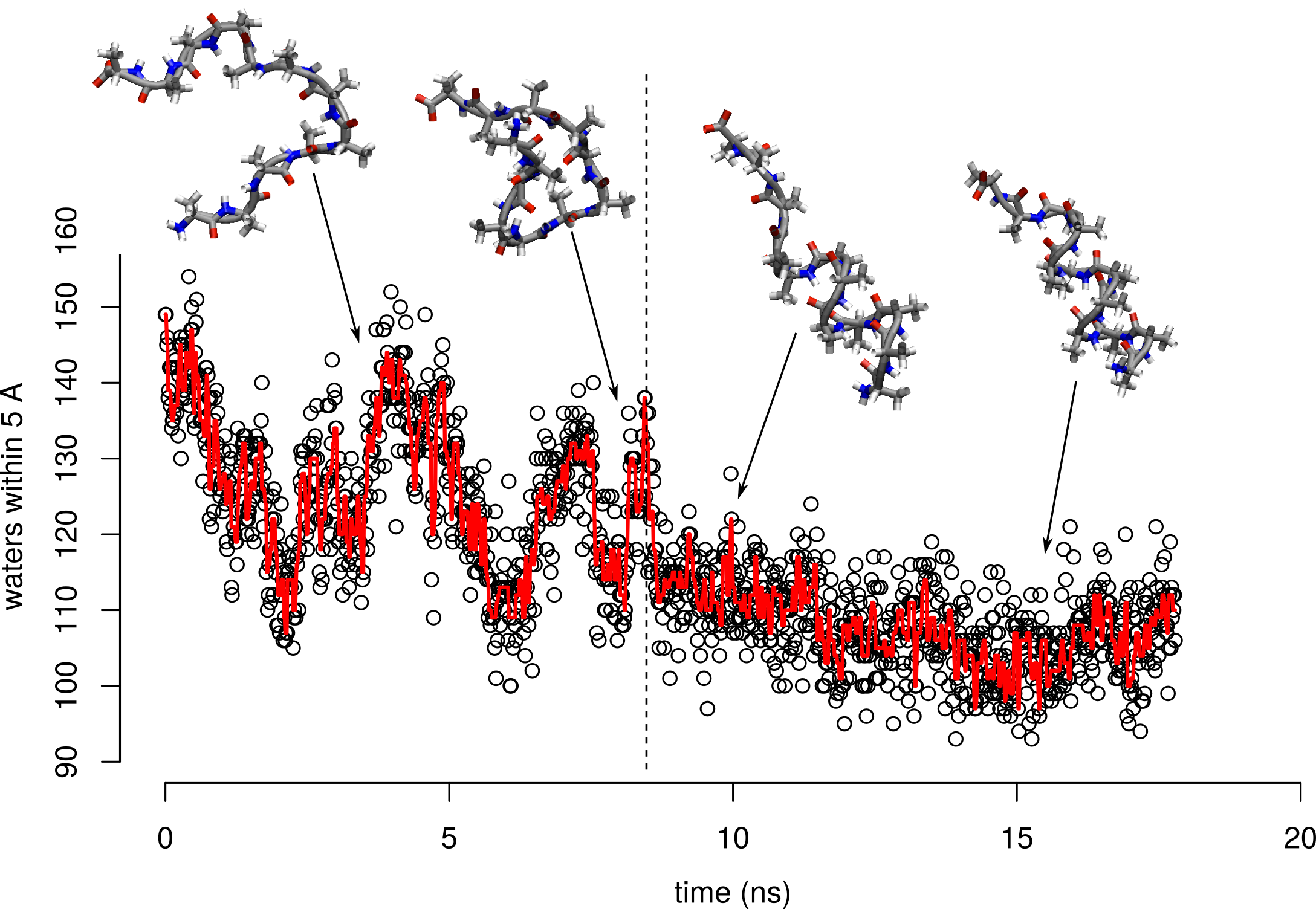
Twelve alanine chain in water, sampled every 12.5 ps

Twelve alanine chain in water, sampled every 12.5 ps. Smoothed.

I'll leave the video up -- now work through the handout in class

After watching the simulation: is formation of a helix thermodynamically favorable or unfavorable?

Favorable (helix forms without outside help)

$\Delta H^{\circ\prime}$: A 12-alanine helix forms 8 backbone hydrogen bonds. If, on average, a protein hydrogen bonds contributes $-20\ kJ\cdot mol^{-1}$ to the enthalpy, what is enthalpy due to hydrogen bonds in the helical state?

$8 \times -20 \ kJ\cdot mol^{-1} = -160 \ kJ \cdot mol^{-1}$

$\Delta S^{\circ\prime}$: The 12-alanine peptide has 24 rotatable bonds (the $^{+}H_{3}N-C_{\alpha}$ and $C_{\alpha}-COO-$ bonds). How many conformations are possible for a 12-alanine peptide?

$3^{24} = 282,429,536,481$

What is the entropy change on folding?

$\Delta S^{\circ \prime} = Rln \Big (\frac{N_{helix}}{N_{unfolded}} \Big )$

$\Delta S^{\circ \prime} = Rln \Big (\frac{1}{282,429,536,481} \Big )$

$\Delta S^{\circ \prime} = -0.22 \ kJ \cdot mol^{-1} \cdot K^{-1}$

$\Delta G^{\circ\prime}$: From these calculations, what would you predict $\Delta G_{unf\rightarrow helix}^{\circ\prime}$ to be?

$\Delta G^{\circ\prime} = \Delta H ^{\circ\prime} - T \Delta S^{\circ\prime}$

$\Delta G^{\circ\prime} = -160 - 300 \times -0.22$

$\Delta G^{\circ\prime} = -94 \ kJ \cdot mol^{-1}$

Let's look at the simulations one more time

What happens to the number of hydrogen bonds over folding?

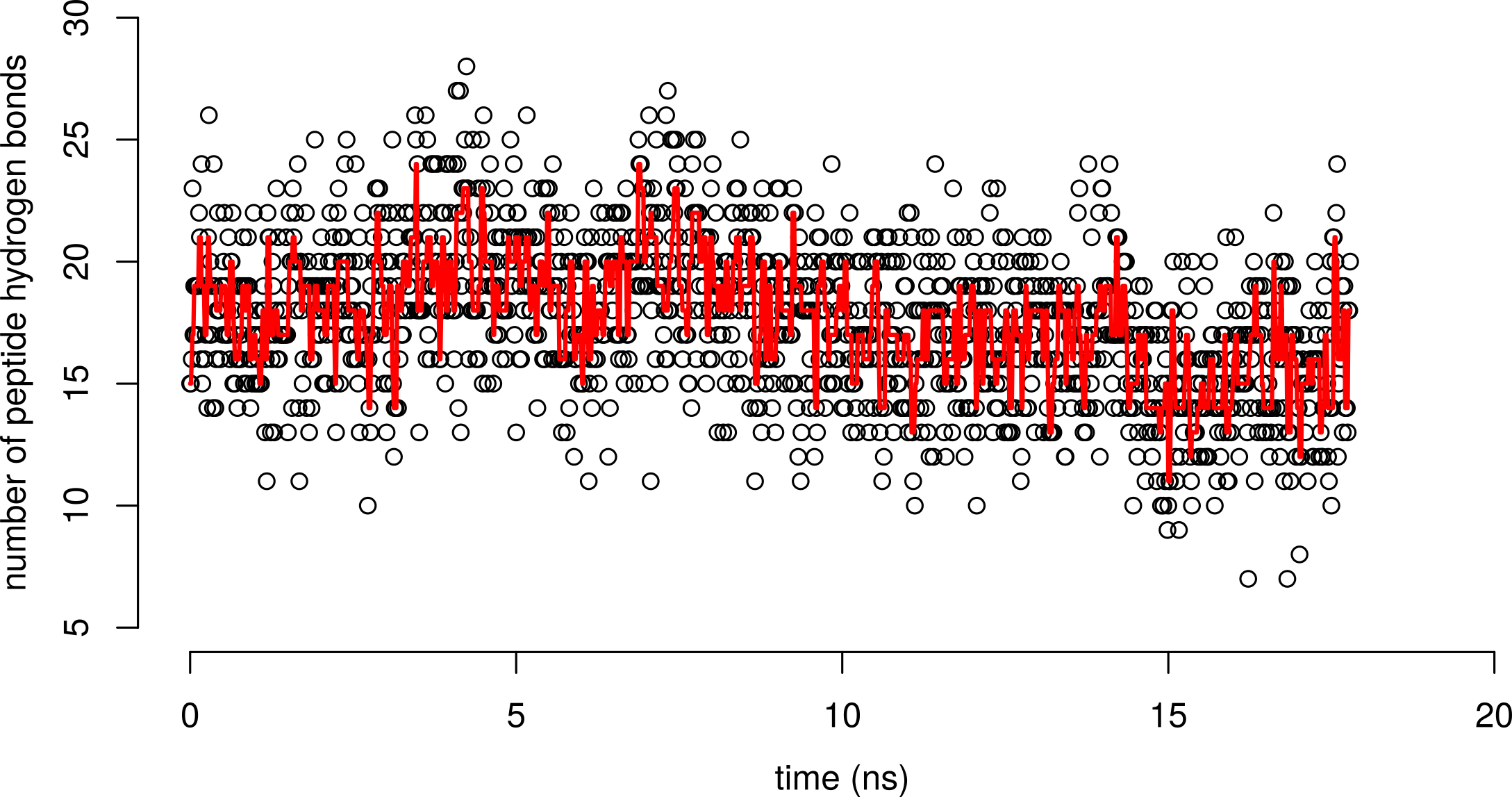
Number of chain hydrogen bonds is about the same between the folded and unfolded states

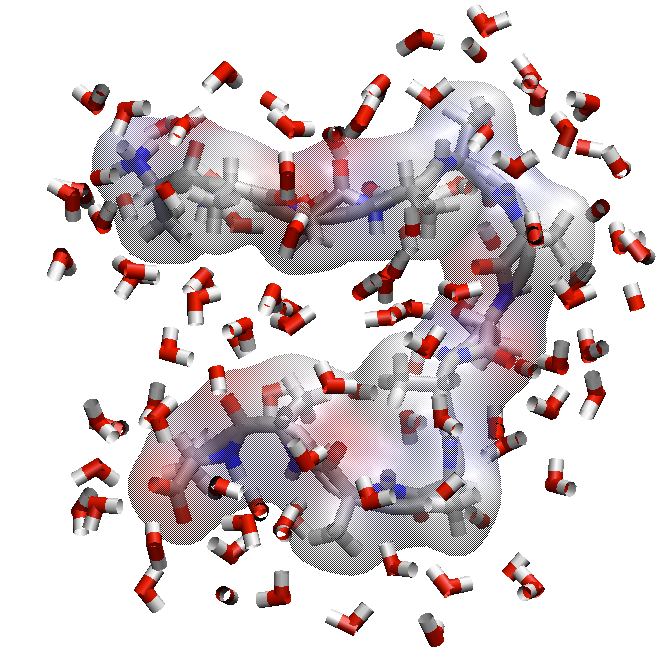
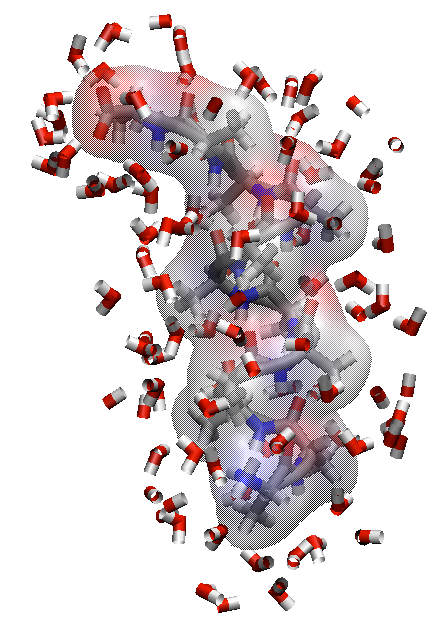
What happens to the water-exposed surface area on folding?

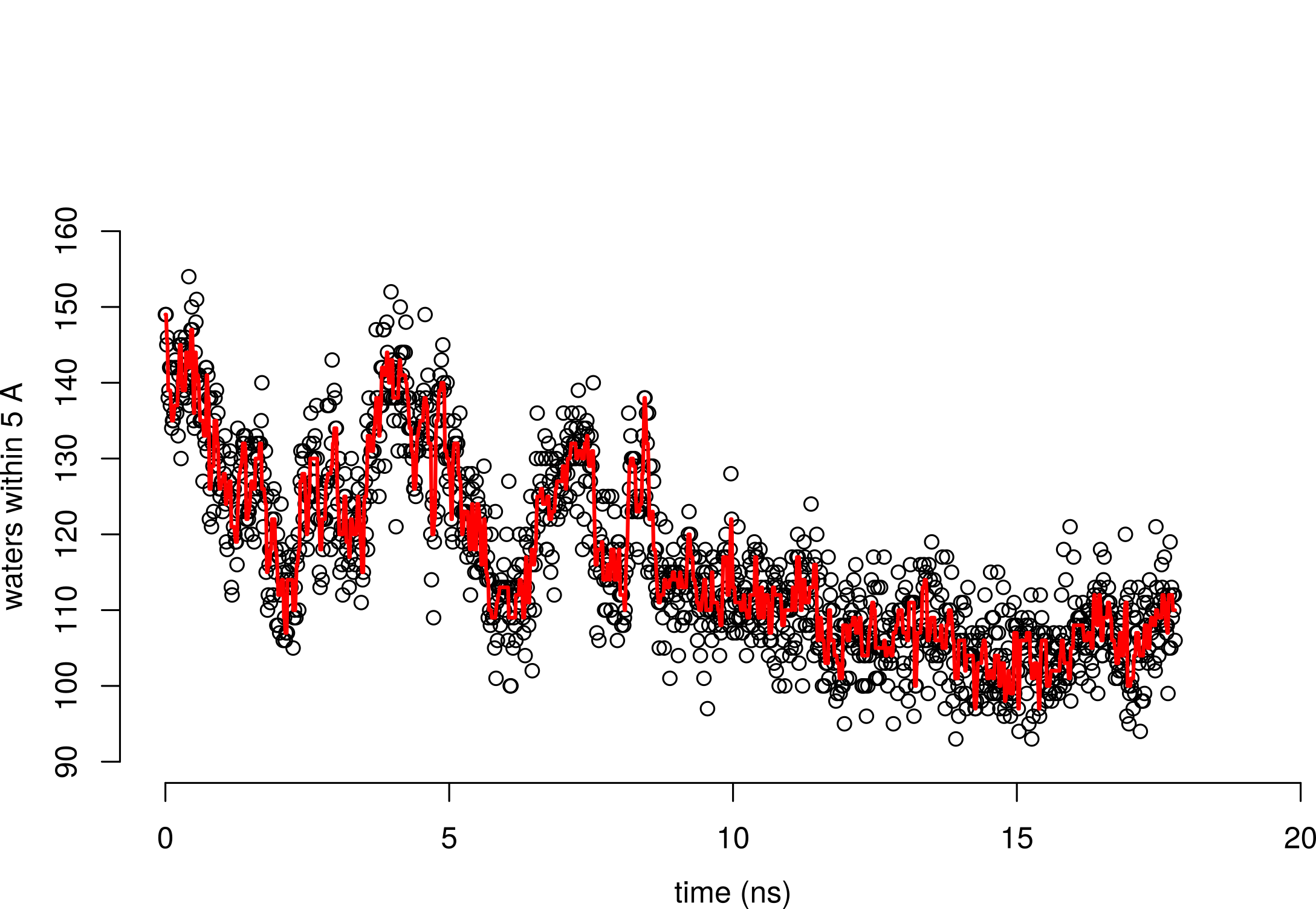
Folded state has less surface area interacting with water

Folded state has less surface area interacting with water

Hand out #2!

Experimental $\Delta G^{\circ\prime}$: If you make a solution of peptides made of 12 alanines at $300\ K$, $80\%$ of the molecules are $\alpha$-helices, $20\%$ are unfolded. What is $\Delta G_{unf\rightarrow helix}^{\circ\prime}$?

$\Delta G^{\circ\prime} = -RTln(K)$

$\Delta G^{\circ\prime} = -RTln\Big ( \frac{helix}{unfolded} \Big )$

$\Delta G^{\circ\prime} = -0.0083 \times 300 \times ln \Big ( \frac{0.8}{0.2} \Big ) $

$\Delta G^{\circ\prime} = -3.5 \ kJ \cdot mol^{-1}$

How does this number compare to your predicted $\Delta G^{\circ\prime}$?

Much worse ($-3.5$ vs. $-94 \ kJ \cdot \ mol^{-1}$)

The experimental value for $\Delta H^{\circ\prime}$ is $-41\ kJ\cdot mol^{-1}$. Assuming $8$ hydrogen bonds actually form and that the hydrogen bonds are the main contribution to $\Delta H^{\circ\prime}$, what is each hydrogen bond “worth” in the helix? Why might this be different from the value we used above?

$-41/8 = -5.1\ kJ\cdot mol^{-1}$

Less than $-20\ kJ \cdot mol^{-1}$ because these hydrogen bonds compete with water hydrogen bonds

Now you know $\Delta G^{\circ\prime}$ and $\Delta H^{\circ\prime}$. What is the contribution of entropy ($T\Delta S^{\circ\prime}$) to the free energy of helix formation? Does entropy favor or disfavor helix formation?

$\Delta G^{\circ \prime} = \Delta H^{\circ \prime} - T\Delta S^{\circ \prime}$

$-3.5 = -5.1 - T\Delta S^{\circ \prime}$

$ 1.6 = - T\Delta S^{\circ \prime}$

Is it bigger or smaller than your prediction?

Smaller.

From calculation: $-300\times-0.22 = 66\ kJ \cdot mol^{-1}$

From experiment: $-1.6 kJ \cdot mol^{-1}$

Minimizing surface area interacting with water favorable releases waters and creates favorable (positive) $\Delta S$.

Folded state has less surface area interacting with water

Hydrogen bonds

$\Delta H^{\circ \prime} = \color{blue}{H^{\circ \prime}_{prot-prot}} - \color{red}{H^{\circ \prime}_{prot-water}}$

$\Delta H^{\circ \prime} = \color{blue}{-25.1 \times 8} - \color{red}{-20.0 \times 8} = -41 \ kJ \cdot mol^{-1}$

Conformational entropy

$\Delta S^{\circ \prime}_{helix} = \color{blue}{S^{\circ \prime}_{helix}} - \color{red}{S^{\circ \prime}_{unfolded}}$

$\Delta S^{\circ \prime}_{helix} = \color{blue}{Rln(1)} - \color{red}{Rln(3^{24})} = -0.22 \ kJ \cdot mol^{-1} \cdot K^{-1}$

$T \Delta S^{\circ \prime}_{helix} = -65.7 \ kJ \cdot mol^{-1}$

Hydrophobic effect

Loss of exposed area increases disorder of water

$\Delta S^{\circ \prime}_{hphobe} = 0.094 \ kJ \cdot mol^{-1} \cdot K^{-1}$ (water release)

$T \Delta S^{\circ \prime}_{hphobe} = 28.1 \ kJ \cdot mol^{-1}$

$\Delta G^{\circ \prime} = \Delta H^{\circ \prime}_{hbond} - T (\Delta S^{\circ \prime}_{helix} + \Delta S^{\circ \prime}_{hphobe})$

$-3.5 = -41.0 - 300(-0.22 + 0.09)$

The stability of a structure is determined by many offsetting terms

• Folding is driven by:
  • Favorable hydrogen bonds (helix makes hydrogen bonds) (enthalpy)
  • Hydrophobic effect (a helix has a surface area less than that of the unfolded state) (entropy)
• Folding is opposed by:
  • Competing hydrogen bonds with water (enthalpy)
  • Loss of conformational entropy