Review session this Wednesday 10/11 from 7-9 pm in Lawrence 115
Some cleanup
The stability of a structure is determined by many offsetting terms
- Folding is driven by:
- Favorable hydrogen bonds (helix makes hydrogen bonds) (enthalpy)
- Hydrophobic effect (a helix has a surface area less than that of the unfolded state) (entropy)
- Folding is opposed by:
- Competing hydrogen bonds with water (enthalpy)
- Loss of conformational entropy
The experimental value for $\Delta H^{\circ\prime}$ is $-41\ kJ\cdot mol^{-1}$. Assuming $8$ hydrogen bonds actually form and that the hydrogen bonds are the main contribution to $\Delta H^{\circ\prime}$, what is each hydrogen bond “worth” in the helix? Why might this be different from the value we used above?
$-41/8 = -5.1\ kJ\cdot mol^{-1}$
Less than $-20\ kJ \cdot mol^{-1}$ because these hydrogen bonds compete with water hydrogen bonds
Key point. You have to consider both unfolded and folded
$\Delta H^{\circ \prime} = \color{blue}{H^{\circ \prime}_{prot-prot}} - \color{red}{H^{\circ \prime}_{prot-water}}$
$\Delta H^{\circ \prime} = \color{blue}{8 \times -25.1} \color{red}{-8 \times -20.0} = -41 \ kJ\cdot mol^{-1}$
$-41 \ kJ\cdot mol^{-1}$ is correct enthalpy to use, not $-5.1$ like I did Friday
How does this play out for $\Delta S$?
From calculation
$\Delta S^{\circ \prime} = Rln(N_{helix}/N_{unfolded})$
$\Delta S^{\circ \prime} = -0.22\ kJ \cdot mol^{-1} K^{-1}$
From experiment
$\Delta G^{\circ \prime} = \Delta H^{\circ \prime} - T \Delta S^{\circ \prime}$
$\Delta G^{\circ \prime} - \Delta H^{\circ \prime} = -T \Delta S^{\circ \prime}$
$\frac{\Delta G^{\circ \prime} - \Delta H^{\circ \prime}}{-T} = \Delta S^{\circ \prime}$
$\Delta S^{\circ \prime} = \frac{-3.5 --41}{-300} = -0.125\ kJ \cdot mol^{-1} \cdot K^{-1}$
It is less entropically unfavorable to collapse helix than you might expect because of the hydrophobic effect
Key point. You have to consider both water and protein
$\Delta S^{\circ \prime}_{helix} = \color{blue}{S^{\circ \prime}_{helix}} - \color{red}{S^{\circ \prime}_{unfolded}}$
$\Delta S^{\circ \prime}_{hphobe} = \color{blue}{S^{\circ \prime}_{folded\ surface}} - \color{red}{S^{\circ \prime}_{unfolded \ surface}}$
$\Delta S^{\circ \prime} = \Delta S^{\circ \prime}_{helix} + \Delta S^{\circ \prime}_{hphobe}$
$-0.125 = -0.22 + \Delta S^{\circ \prime}_{hphobe}$
$0.095 \ kJ \cdot mol^{-1} \cdot K^{-1}= \Delta S^{\circ \prime}_{hphobe}$
Hydrophobic effect makes favorable entropic contribution to folding
Where does $S = Rln(N)$ come from, anyway?
Proline and glycine are both known as "secondary structure breakers"
Why might this be the case?
Proline uses the backbone nitrogen as part of its R-group. No hydrogen bonds + kink
Glycine has a H for an R-group. It's floppy and entropically expensive to immobilize
Disulfide bonds form between ___________ residues. These _________ [covalent|ionic|hydrogen bond] interactions ____________ [stabilize|destabilize] protein structure
Disulfide bonds form between cysteine residues. These covalent interactions stabilize protein structure
The Protein Folding Problem
2017-10-09
Conceptual goals
- Understand that the folded structure of the protein is the free energy minimum for the chain
Skill goals
- Manipulate thermodynamic equations describing protein stability to calculate contributions of different forces
- Reason correctly about interactions by thinking correctly about both sides of a reaction coordinate
- A 100 amino acid protein will have 198 peptide bonds. If each bond can take 3 possible conformations, how many conformations are there?
- If each bond rotates every nanosecond, how long would it take for the protein to sample all possible structures?
- $3^{198} = 3\times 10^{94}$ conformations
- $3\times 10^{94}\ conf \times \frac{1 \times 10^{-9} \ s}{conf} = 3 \times 10^{89} \ s$
- $9 \times 10^{77} years$
Real proteins fold in milliseconds
What does this tell us about protein folding?
Folding does not proceed by random search.
Proteins fold by a biased search.

Previous steps set up next steps
- Local elements fold (like secondary structure) fold
- These folded elements change environment of rest of chain
- Other local parts of the structure fold
- Settles in to a final 3D fold
This is known as a "folding funnel"
We can follow folding directly with Hydrogen-Deuterium Exchange Mass Spectrometry
 Walter Englander
Walter Englander
We can follow structural intermdiates with molecular dynamics simulations
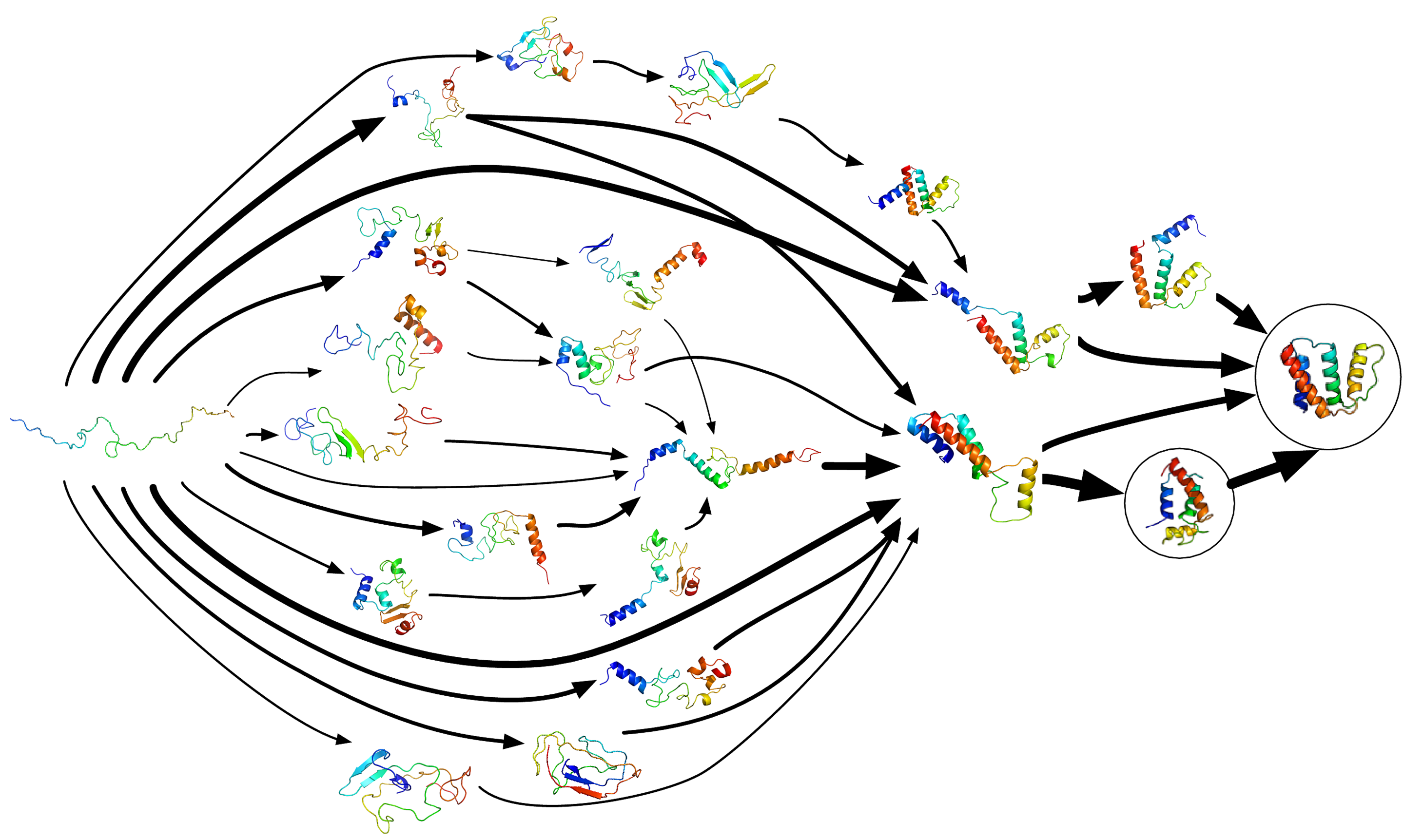 Vijay Pande
Vijay Pande
We can design proteins from scratch
 Brian Kuhlmann
Brian Kuhlmann
George Rose is a well-known protein folder at Johns Hopkins
He is giving a seminar at 2 pm today, in Willamette 240.
Fun fact: cookies and coffee at 1:45
Fun other fact: George calls funnels the F-word
Summary
- To understand biochemical reactions, you need to account for both sides of the reaction
- To understand biochemical reactions, you need to account for biomolecules and water
- Proline, Glycine and Cysteine are special amino acids, altering secondary structure (Pro,Gly) or forming covalent bonds (Cys)
- Proteins do not fold randomly, but follow a "folding funnel" to the lowest energy state