Enzymes as catalysts
2017-10-16
The next four classes
- Enzymes as catalysts
- Mechanism of serine protease
- Michaelis-Menten kinetics
- Enzyme regulation
Substrate binds at enzyme active site.
Enzymes are catalysts that speed up reactions without being consumed themselves
What determines how fast this reaction can go? (and why?)
Getting to the transition state, because that is the most unfavorable (most unlikely) state in the reaction.
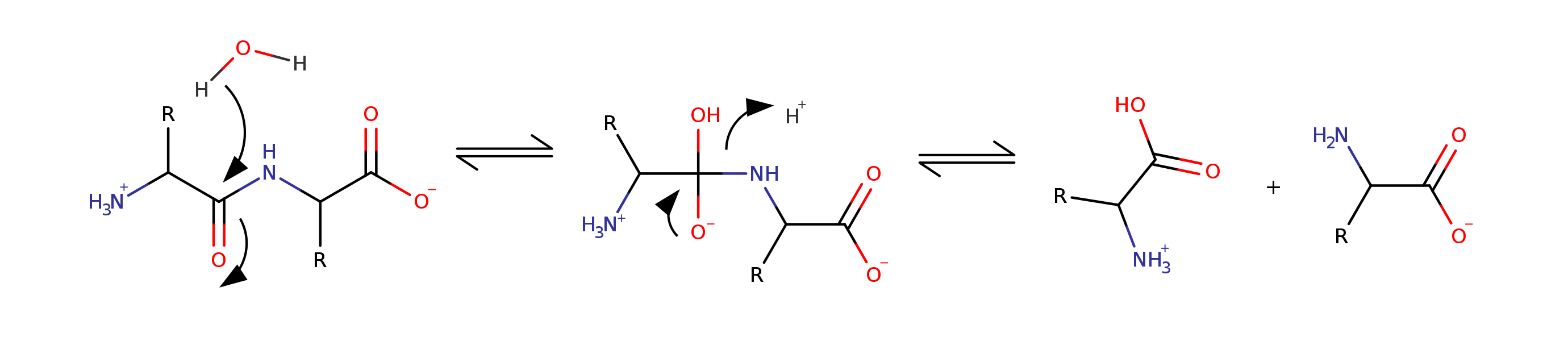
Hydrolysis of peptide bond has $\Delta G < 0$, but it's slow
rate constant = $k = 1.5 \times 10^{-9}\ s^{-1}$
$k = 0.05\ years^{-1}$. That means 20 years to break a bond!
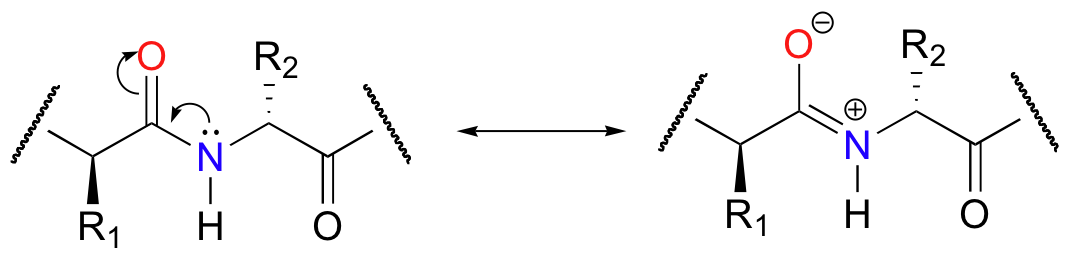
(resonance structure stabilizes substrate structure)
Conceptual goals
- Understand the energetic basis for the rate increases achieved by enzymes (in terms of a free energy reaction coordinate).
Skill goals
- Reason about how changes in free energy reaction coordinate lead to altered reaction rates.
- Manipulate basic Arrhenius equation to quantitatively relate changes in $ E_{a} $ to changes in rate.
Peptide hydrolysis goes from $k = 1.5 \times 10^{-9}\ s^{-1}$ in water (pH 7) to $k = 120\ s^{-1}$ with enzyme
A 100-billion-fold speed up. Once every 20 years to 120 times per second!
How much does the enzyme lower the energy barrier for this reaction?
This is an important step for figuring out how the enzyme works
You are given a single, six-sided dice.
- What is the rate at which you roll sixes?
- What determines the rate?
- How can you increase the rate?
Rate of rolling sixes:
$k_{6} = k_{rolling} \times P_{6}$
If you roll a fair dice once per second, you get a rate of:
$k_{6} = 1\ s^{-1} \times \frac{1}{6} = 0.167\ s^{-1}$
Rate is determined by rolling rate and probability of 6
To speed up the rate, roll faster or weight the dice
For the reaction $E + S \rightleftarrows E \cdot S \rightleftarrows E + P$:
If the rate-limiting step is formation of $E \cdot S$, then we're interested in the left side
$k_{E\cdot S} = k_{try} \times P_{E+S\rightarrow E\cdot S}$
Big point:
A small change in the transition state free energy can lead to large change in rate
(A change worth a few hydrogen bonds gives a 100-billion fold speed up)
How this is done mechanistically:
Construct a "path" of low energy intermediates to overcome the energy barrier
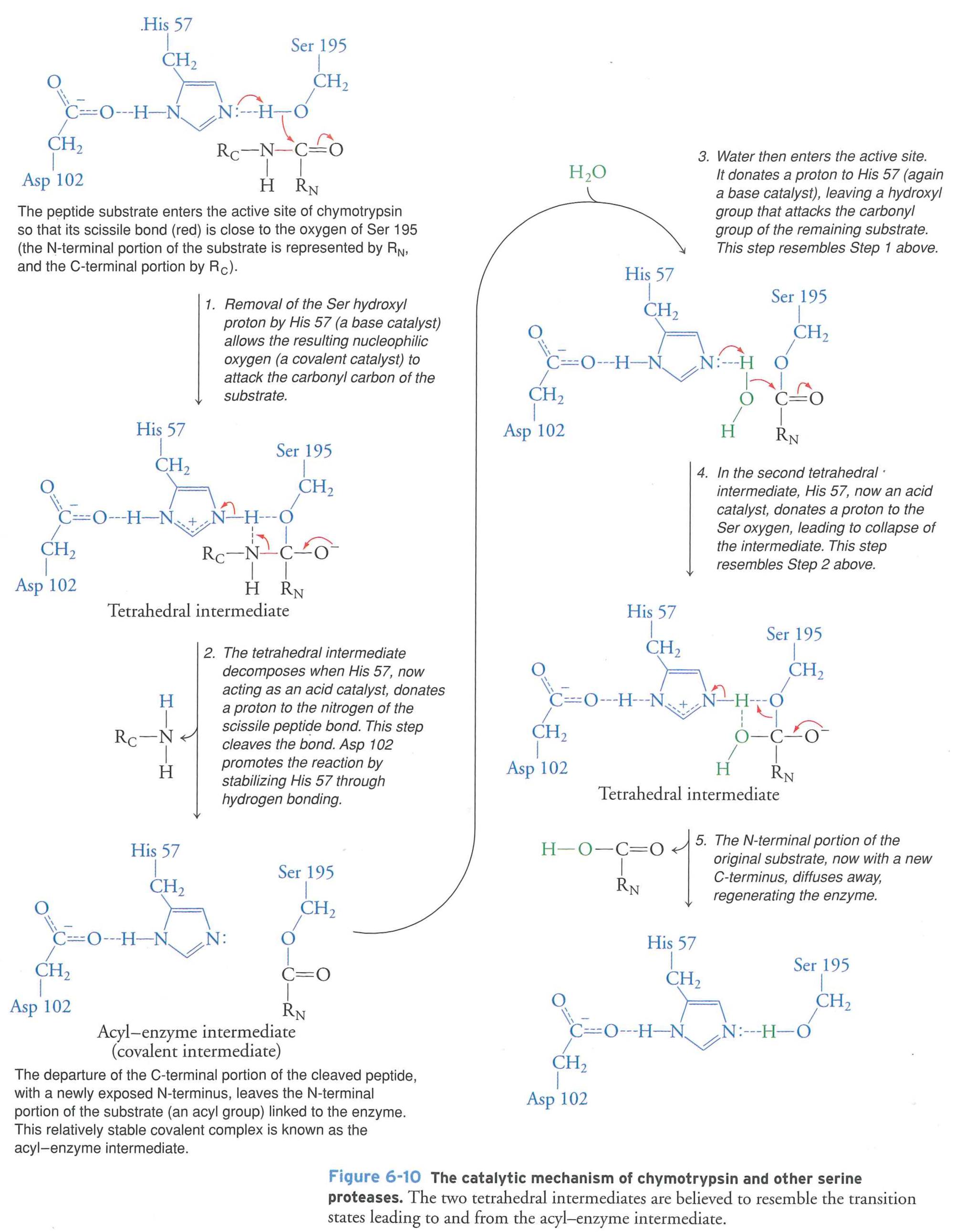
Key points
- Reaction rates are limited by the transition state free energy
- Enzymes speed up rates by lowering the energy barrier (small change in $E_{a}$, big change in rate)
- Transition states are high energy because they are chemically "wacky"
- Enzymes stabilize the transition state, lowering the energy barrier and increasing the rate
- Enzymes can only speed up spontaneous ($\Delta G < 0$) reactions