Enzyme regulation

2017-10-23

Conceptual goals

• Understand how experimental rate measurements allow determination of MM parameters
• Understand how cells tweak these parameters to achieve regulated activity

Skill goals

• Interpret experimental graphs for MM enzymes in terms of altered MM parameters.
• Interpret changes to those parameters in terms of altered underlying chemistry.

The Michaelis-Menten equation:

$$V_{0} = k_{cat}[E]_{T}\frac{[S]_{0}}{[S]_{0} + K_{M}}$$

$V_{0} = k_{cat}[E]_{T}\frac{[S]_{0}}{[S]_{0} + K_{M}} \times \frac{1/[S]_{0}}{1/[S]_{0}}$

$V_{0} = k_{cat}[E]_{T}\frac{1}{1 + K_{M}/[S]_{0}}$

initial velocity = (intrinsic rate of enzyme)(total enzyme)(fraction of enzyme saturated with substrate)

Review: the mechanism of serine protease

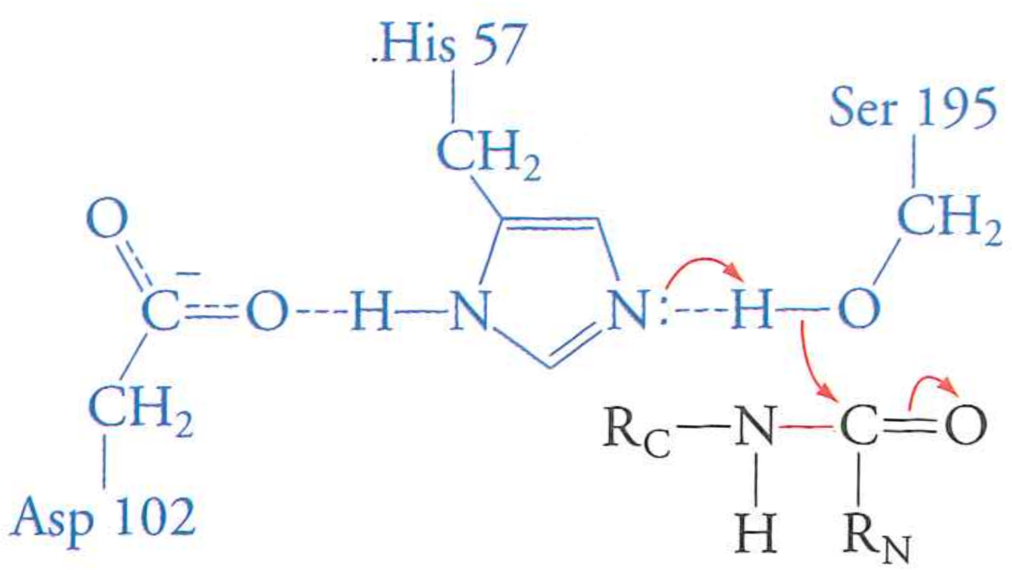
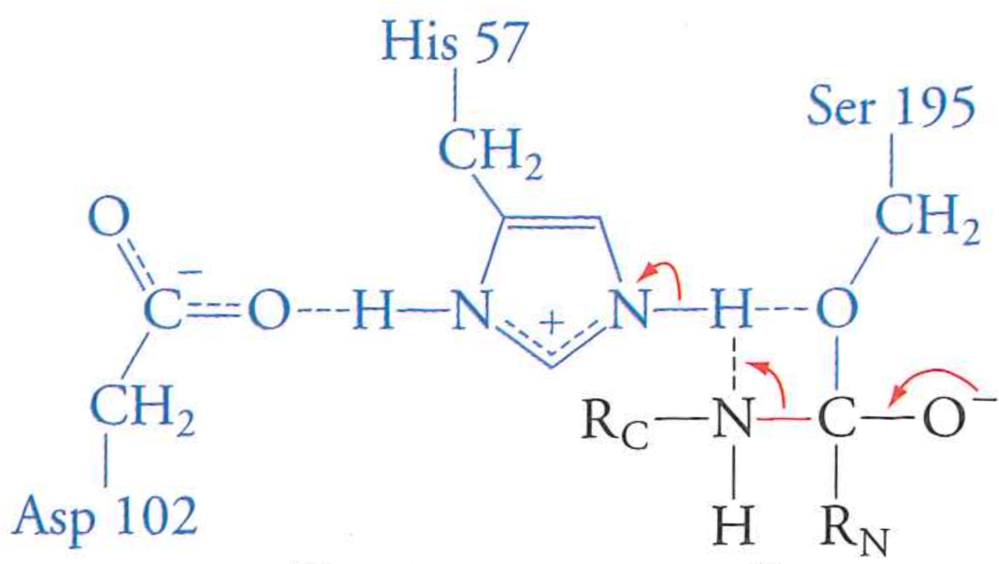
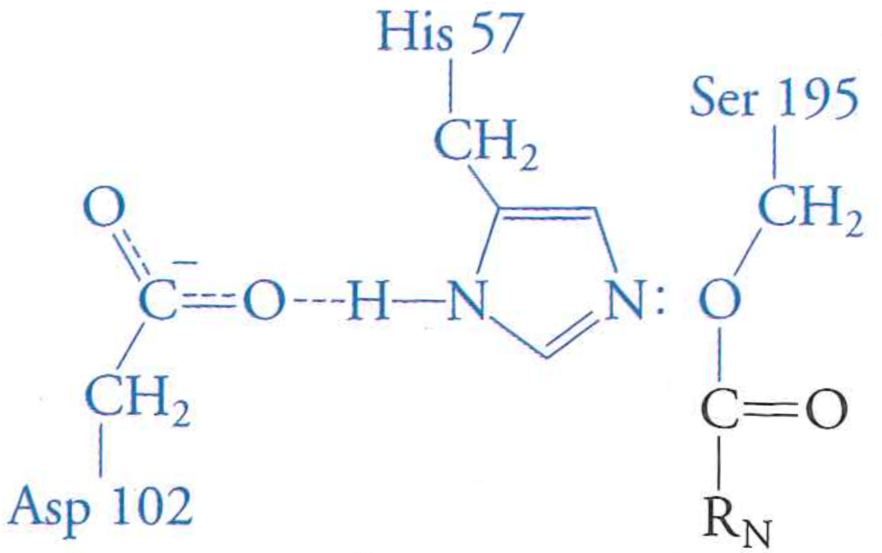
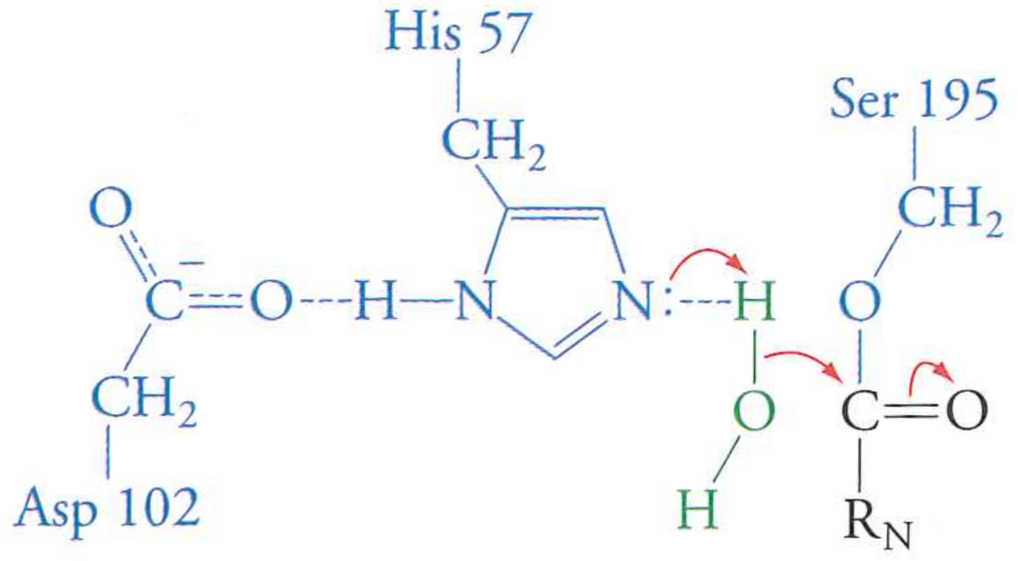
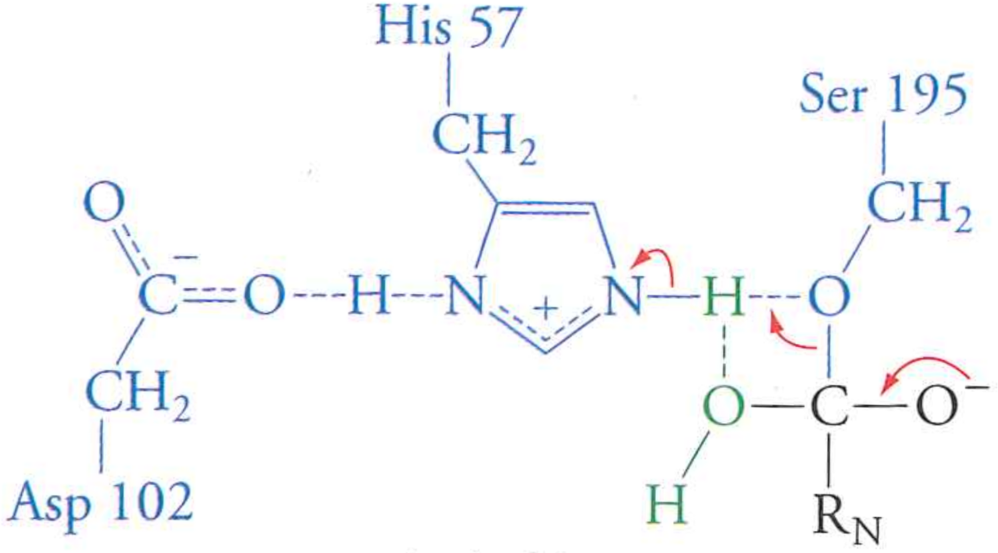
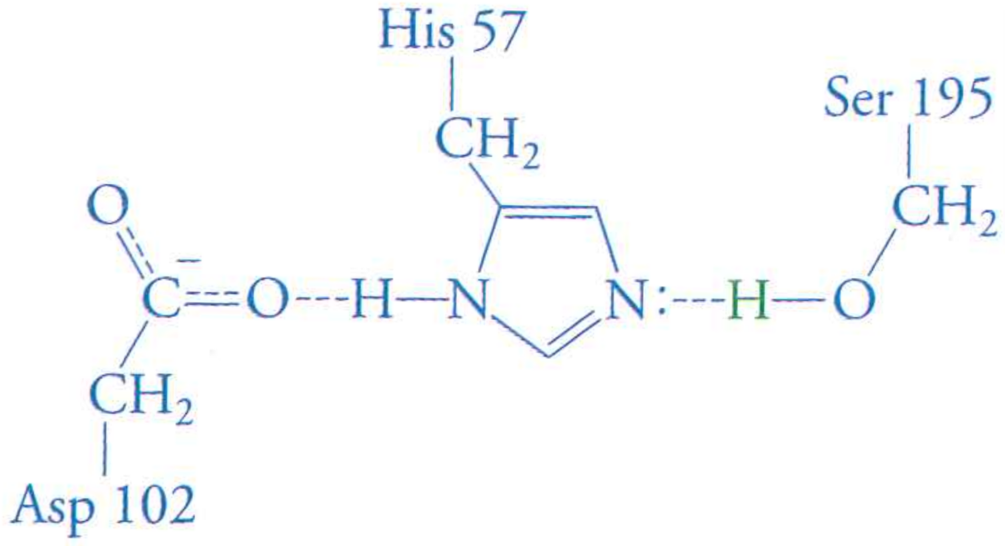
What happens if we mutate Aspartic Acid 102 to an Alanine?

• To transtion state free energy? Raises it
• To $k_{cat}$? Lowers it (slower enzyme)
• To $K_{M}$? No effect

Binding affinity ($K_{M}$) and specificity is determined by interactions just outside active site

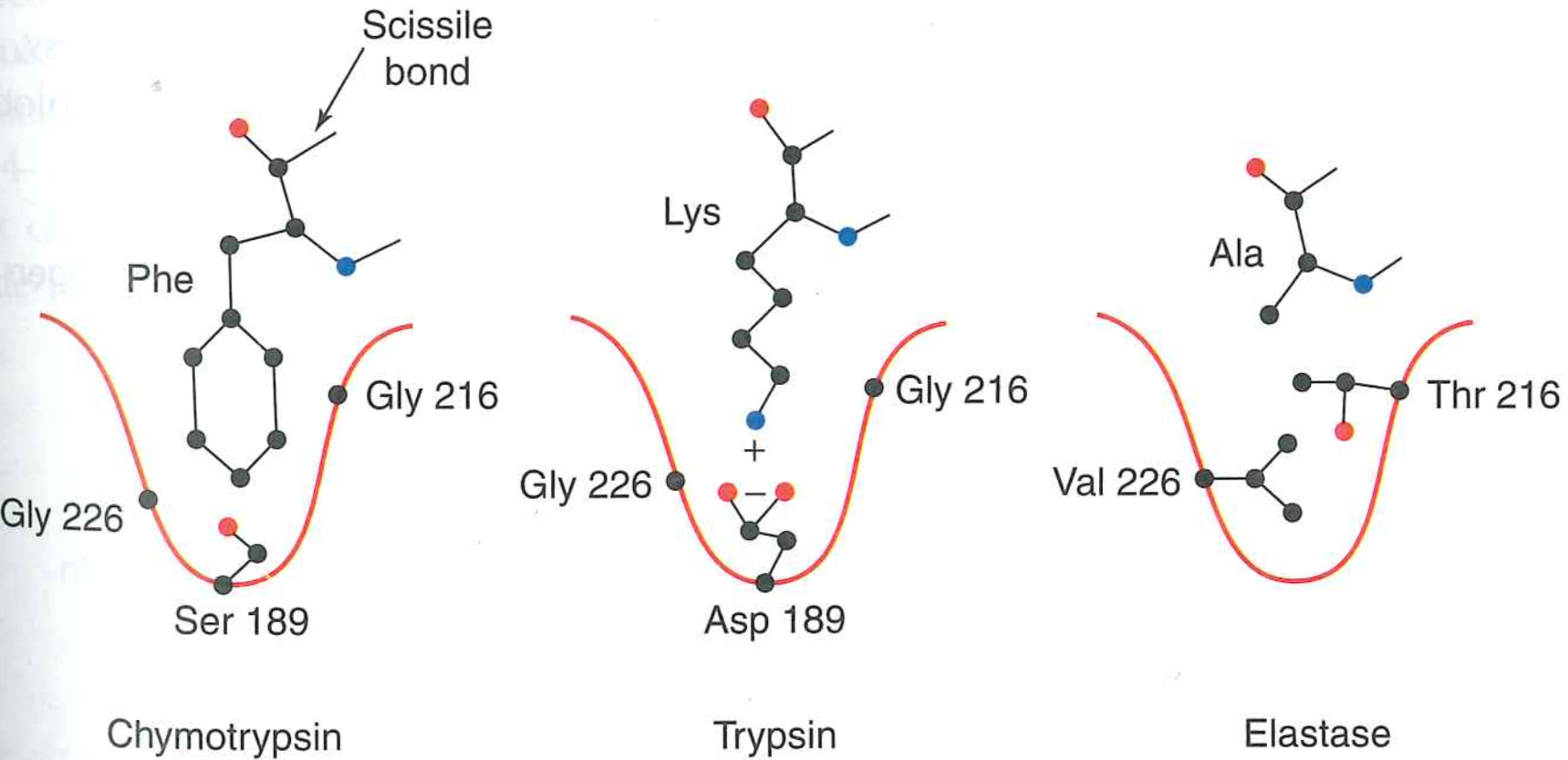
Rule of thumb: change to the active site residues alters $k_{cat}$, while a change to the binding residues alters $K_{M}$.

How can enzymes be regulated without introducing mutations?

$V_{0} = k_{cat}[E]_{T}\frac{[S]_{0}}{[S]_{0} + K_{M}}$

HIV protease inhibitor binds at the enzyme active site

A competitive inhibitor competes for the same site as the substrate and thus slows the enzyme down.

This leads to a increase in: $K_{M}$

The inhibitor usually looks quite similar to the substrate but is less reactive

If you drink moonshine, doctors might give you even more alcohol!

Methanol ($CH_{3}OH$) is not poisonous, but is converted to the potent poison formaldehyde ($CH_{2}O$) by the enzyme alcohol dehydrogenase. One treatment for methanol poisoning is to give the patient copious quantities of ethanol ($CH_{3}CH_{2}OH$). Why might this be?

Ethanol competes with methanol at this site, lowering the rate of formaldehyde production.

Does this alter $k_{cat}$ or $K_{M}$? $K_{M}$ because it competes for the same site.

Sarin is a potent neurotoxin

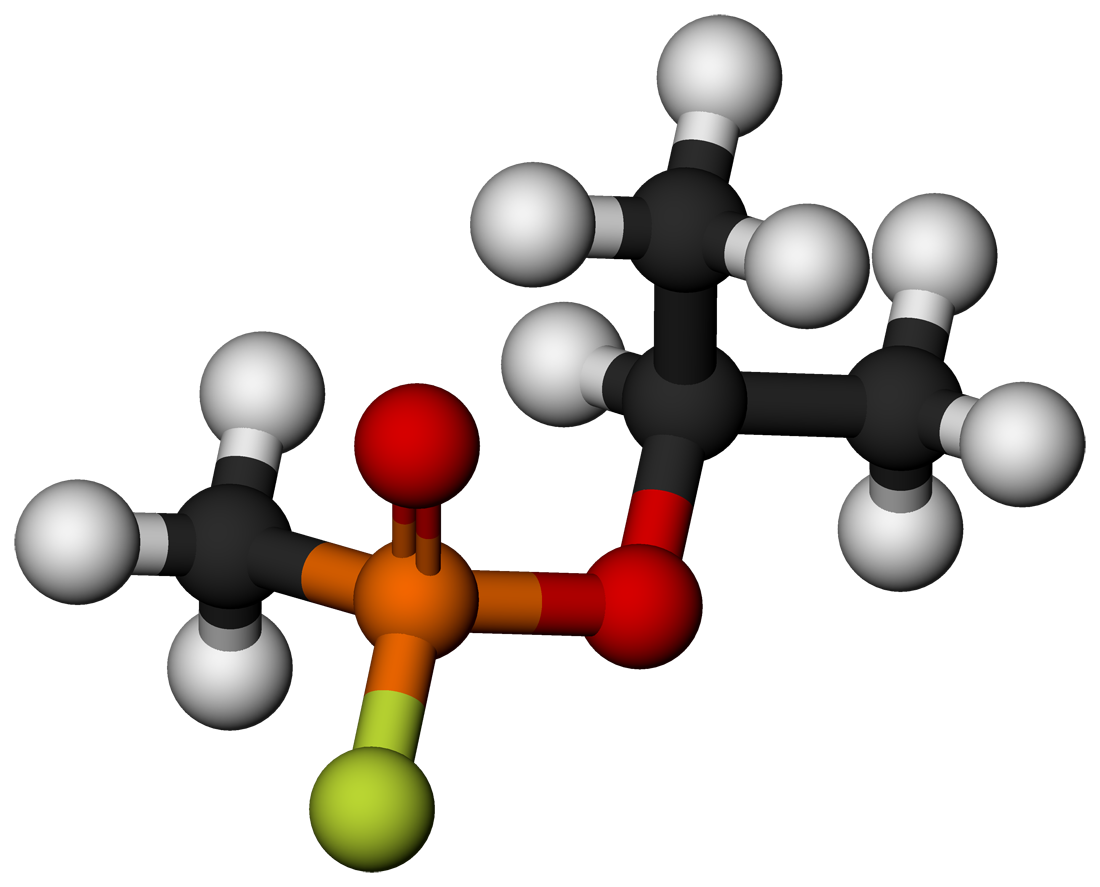
Sarin covalently modifies an active-site serine in acetylcholine esterase

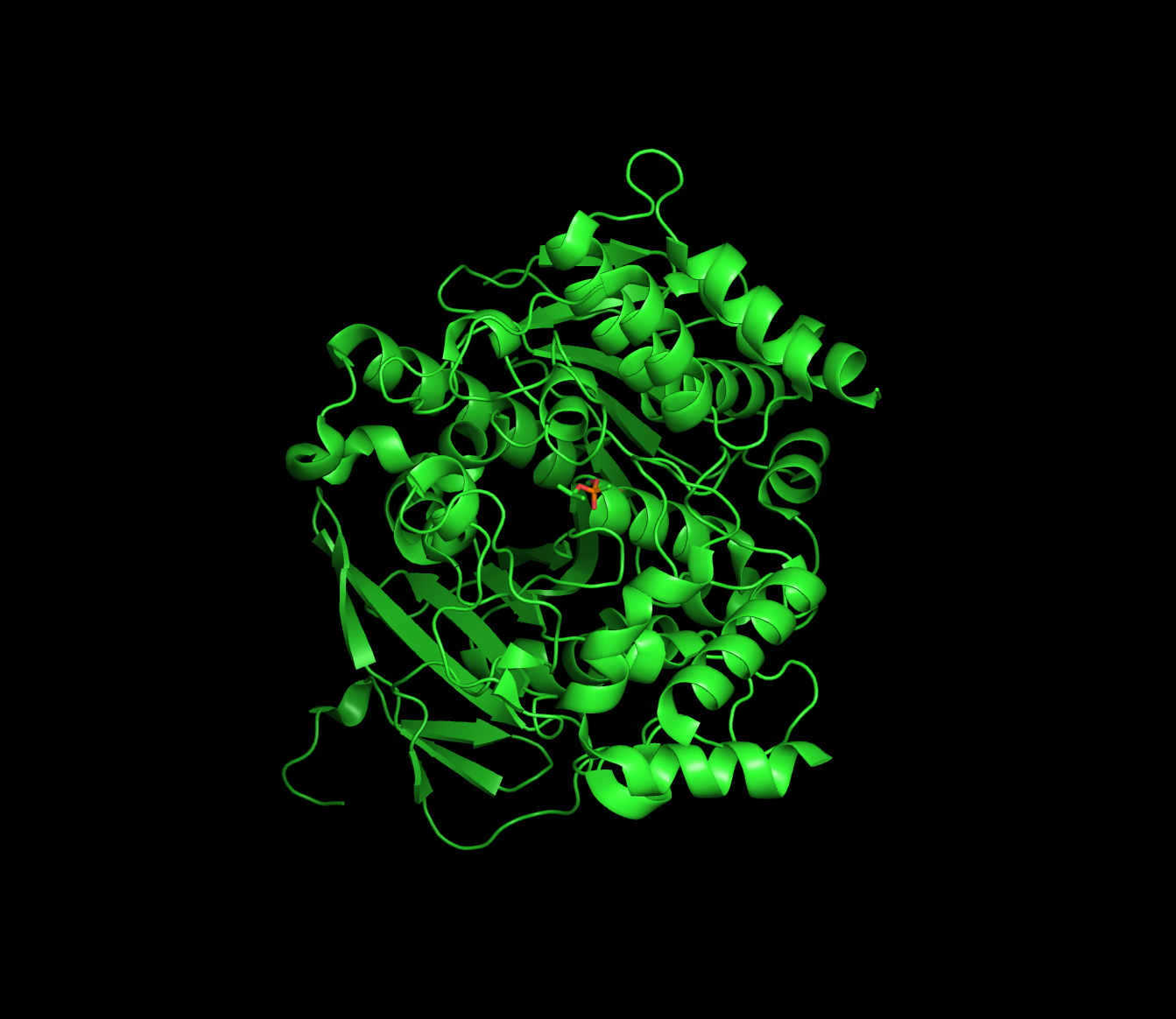
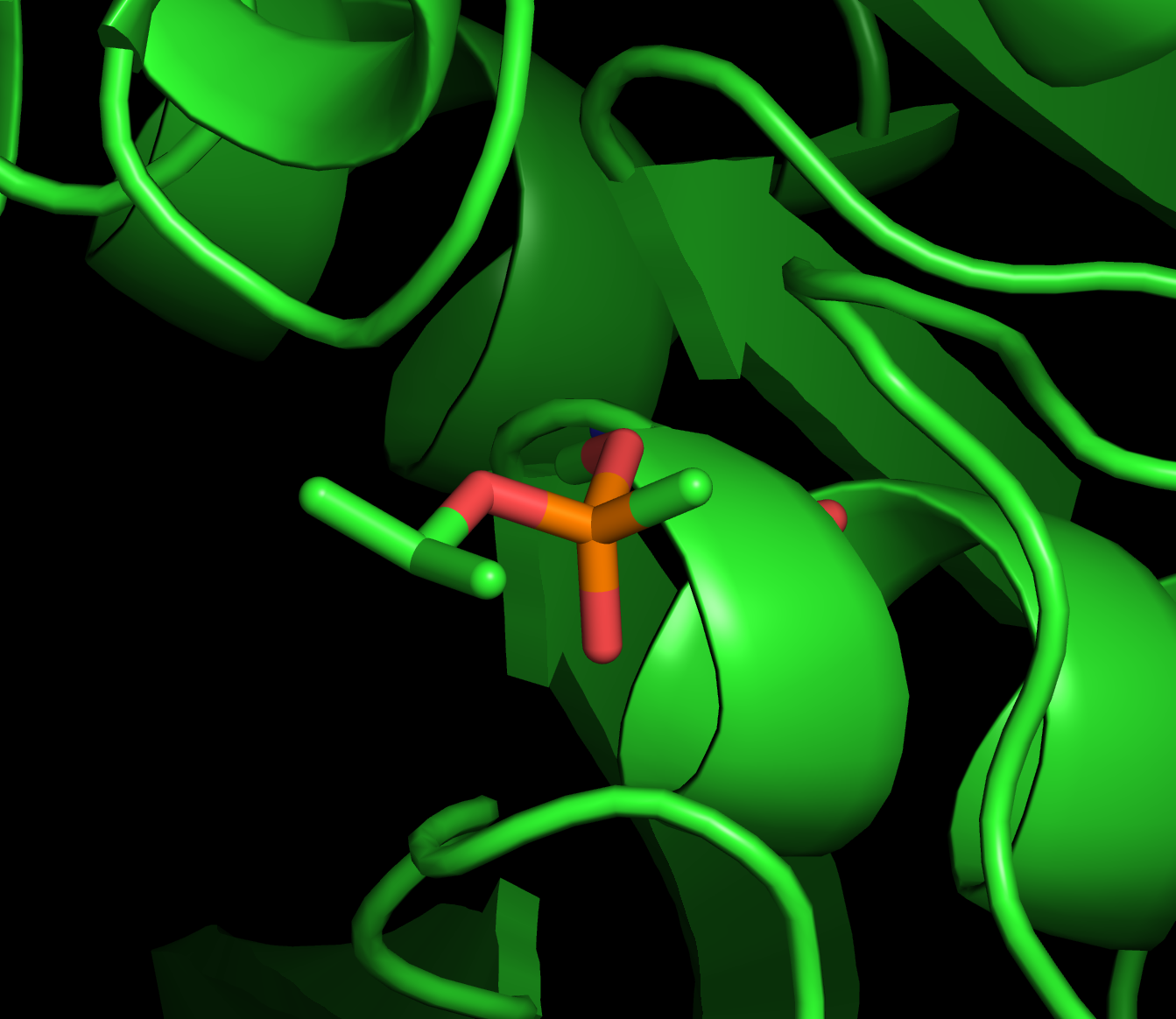
An irreversible or (suicide) inhibitor covalently modifies the active site, destroying the enzyme.

This leads to a drop in: $[E]_{T}$

The inhibitor usually looks quite similar to the substrate

Hepatitis C Virus RNA polymerase binds RNA in its active site

A non-competitive inhibitor inhibits activity by binding away from the active site

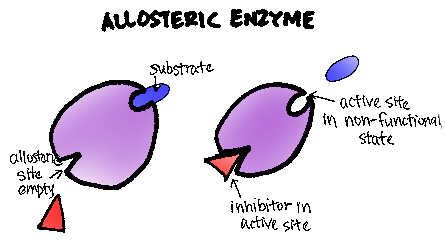
A noncompetitive inihibitor binds distant from the active site, altering active site to turn off activity

This leads to a drop in: $[E]_{T}$. Less of the enzyme is in the active form.

The inhibitor need not have any chemical similarity to the substrate

Foreshadowing: this is through linked equilibria

$E_{active} + I \rightleftarrows E_{inactive} + I \rightleftarrows E_{inactive} \cdot I$

$[E]_{active} = [E]_{T}\theta_{active}$

$\theta_{active} = \frac{[E_{active}]}{[E_{active}] + [E_{inactive}] + [E_{inactive}\cdot I]}$

This "allosteric" mechanism can also be used to turn on an enzyme: binding at a distant site puts enzyme in active form

This leads to an increase in $[E]_{T}$

Summary

• A competitive inhibitor binds at the active site and competes with substrate. This raises $K_{M}$
• A suicide inhibitor irreversibly (covalently) modifies the active site and destroys the enzyme. This lowers $[E]_{T}$
• A Non-competitive inhibitor binds away from the active site and "magically" lowers activity. This lowers $[E]_{T}$
• Cells also directly control how much enzyme they make, altering $[E]_{T}$.

• All of these mechanisms are used biologically and in medicine.