Cooperativity: how does hemoglobin load and unload oxygen?
2017-10-25
Conceptual goals
- Understand how multiple subunits working in conjunction give tightly controlled loading and unloading of cooperative proteins.
Skill goals
- Reason about the thermodynamics of cooperativity using linkage thermodynamics.
- Interpret graphical representations of loading/unloading curves in terms of cooperative behavior.
Globins are proteins that bind $O_{2}$ using a "heme" group with a bound $Fe(II)$ and a proximal His

Credit: Ordway & Garry (2004) JEB 207:3441-3446
Hemoglobin transports $O_{2}$ from the lungs to tissues
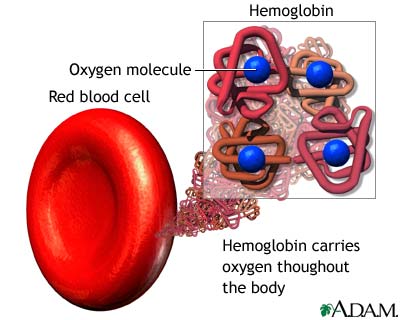
stephaniefuturedoc
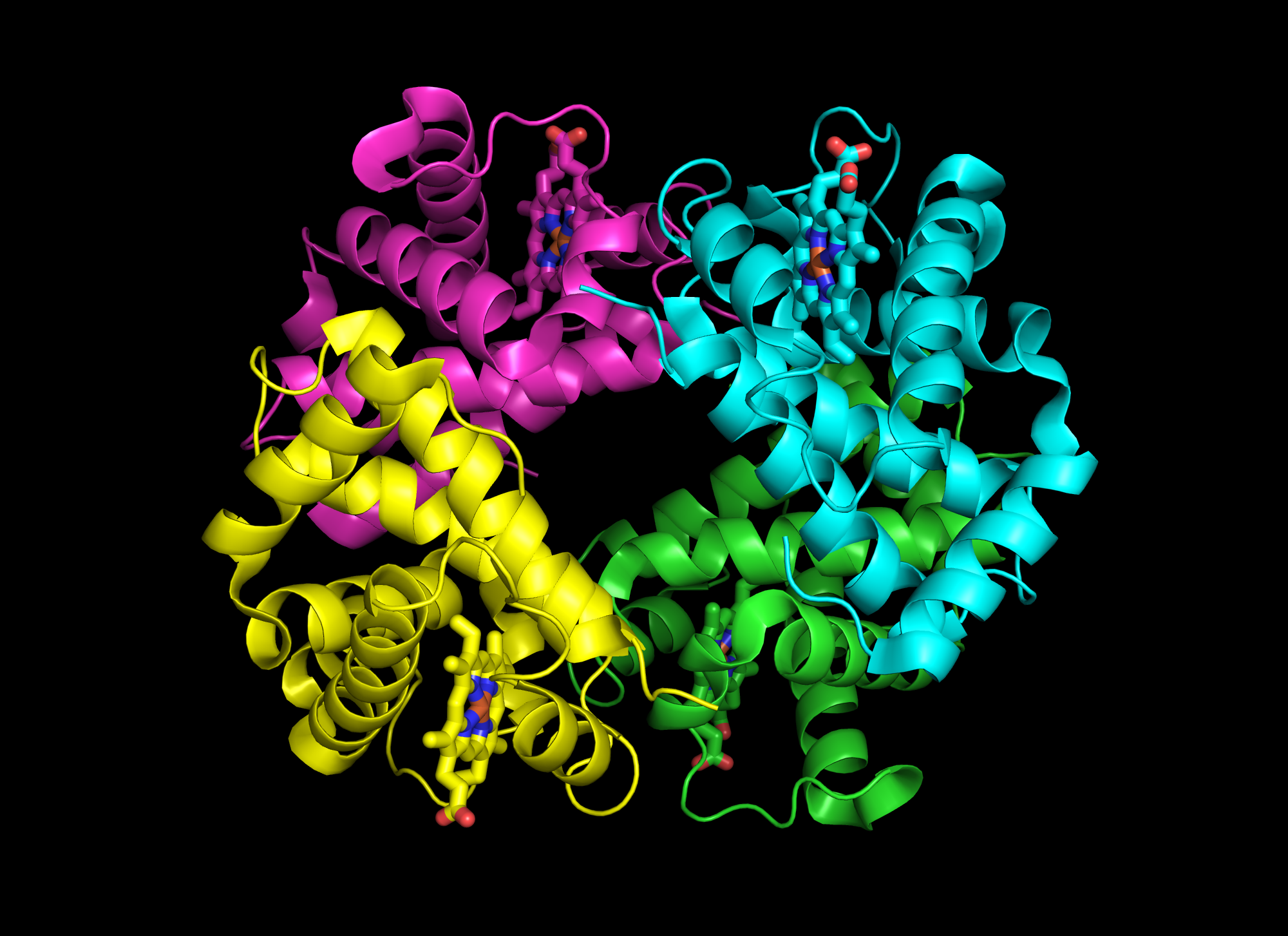
Hemoglobin is a tetramer four proteins
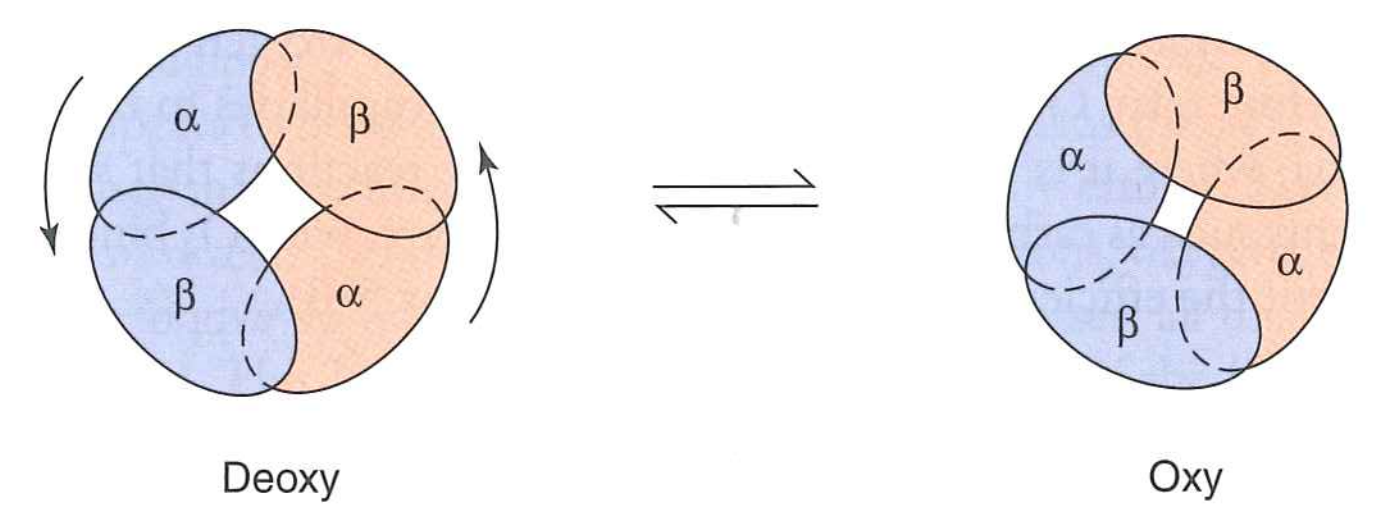
Transition is cooperative (either one state or other -- no intermediate state)
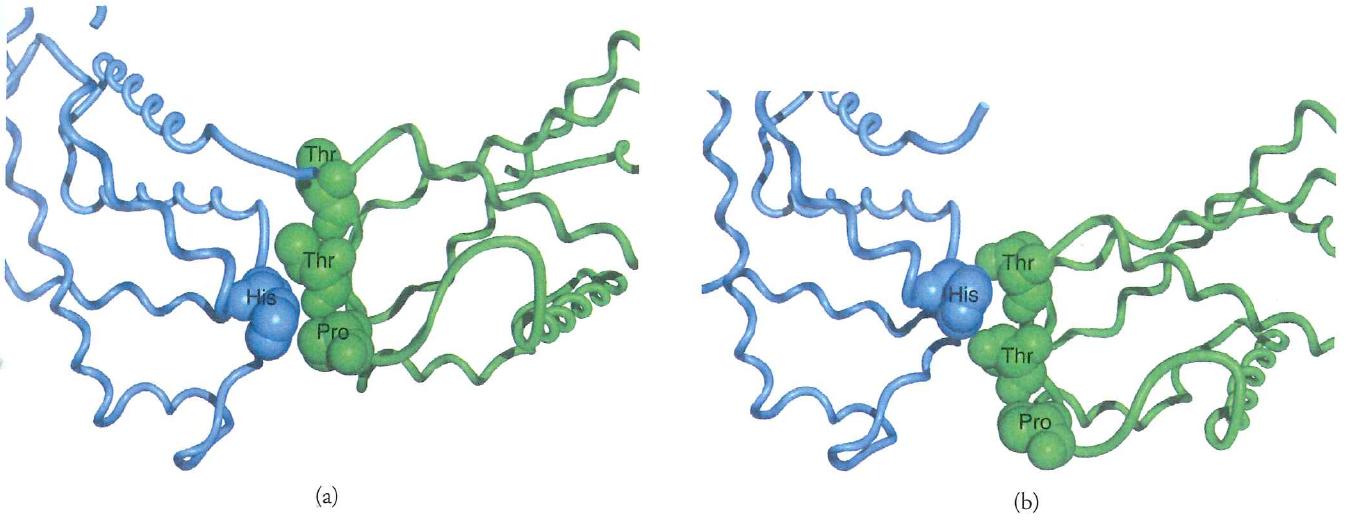
Interfaces lead to cooperativity by linking subunits
Summary I
- Myoglobin and hemoglobin are $O_{2}$ binding proteins that bind $O_{2}$ using a "heme" group
- Hemoglobin is a tetramer of myoglobin-like subunits
- Myoglobin buffers $O_{2}$ in tissues, hemoglobin transports $O_{2}$ in the blood
- Myoglobin would unload at most 10% of its $O_{2}$ if it transported oxygen
- Best monomer ($K_{D}=44\ torr$) could unload 40% of its oxygen
Summary II
- Cooperativity between sites allows hemoglobin to unload 75% of oxygen
- Cooperativity comes about because binding the first $O_{2}$ "pays" to put complex into high $O_{2}$ affinity state.
- This is descibed by the "Hill equation":$$\theta_{Hill} = \frac{1}{1 + (K_{D}/[L])^{n}}$$ where $n$ is $\approx$ number of sites