ATP synthase

2017-11-27

Conceptual goals

• Understand the mechanism of ATP synthase
• Understand the energetics of ATP synthesis

Skill goals

• Reason about energy transduction (and how it can be disrupted).

Oxidative phosphorylation overview:

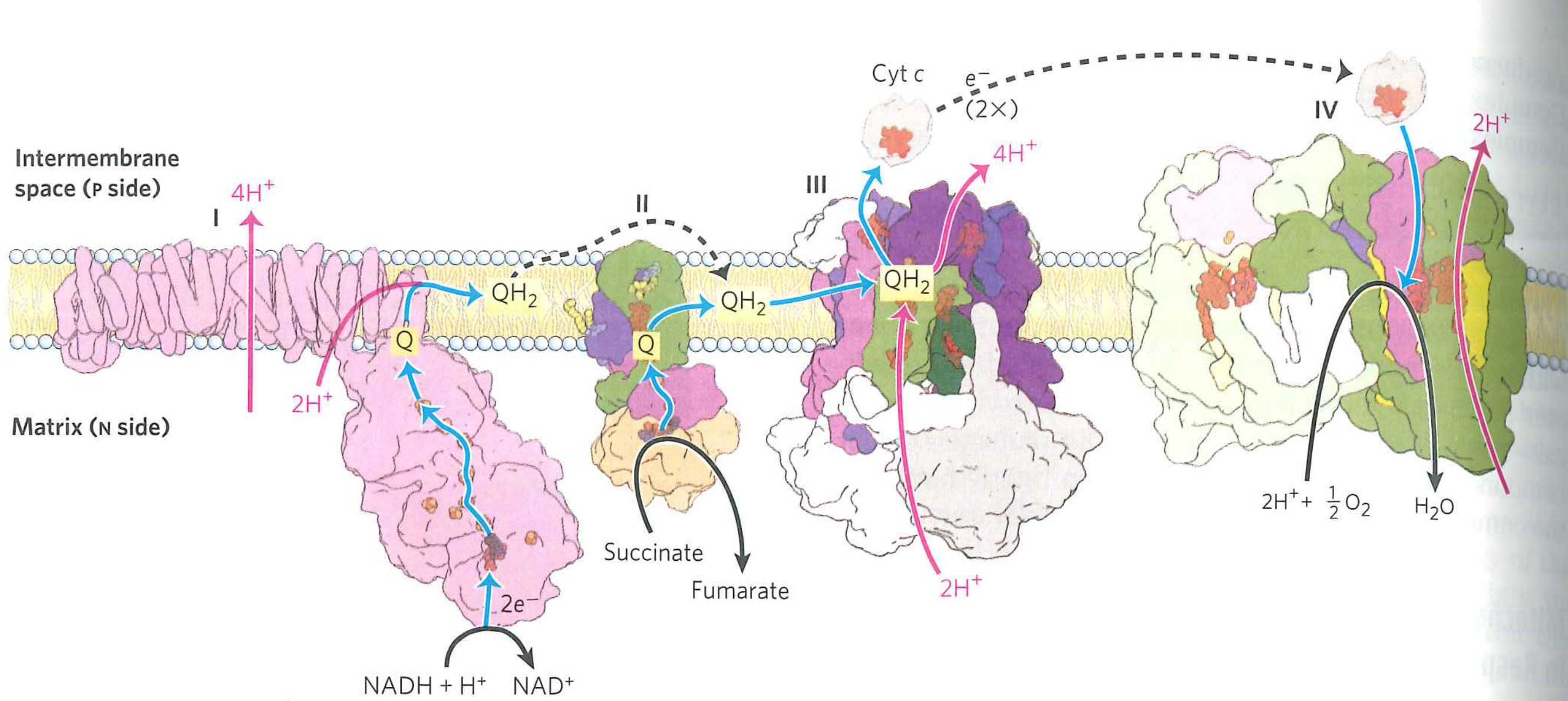
What do we do with the proton gradient?

How does a hydroelectric dam generate electricity?

• Elevated water has potential energy
• Water flows through "penstock," trading potential for kinetic energy
• Moving water pushes on asymmetrical turbine blades, converting linear motion into torsional motion
• Wire moving through a magnetic field induces a change in electron potential (voltage)

This is how an ATP synthase works energetically

This is NOT how this protein works mechanically

How does ATP synthase generate ATP?

• Electron transport pushes protons across the bilayer, generating a potential energy difference across membrane
• Protons flow through the $F_{0}$ subunit, moving through asymmetrical channel and converting potential gradient to rotation
• Rotating shaft alters conformation of cooperative $F_{1}$ subunits, causing alternation between three states
• Alternating conformations push enzyme through enzymatic cycle to catalyze $ADP + P_{i} \rightarrow ATP$ reaction

ATP synthase is mechanical but not inertial. Protons don't "push" on turbine; $F_{1}$ does not "mash" $ADP$ and $P_{i}$ into $ATP$.

Outline:

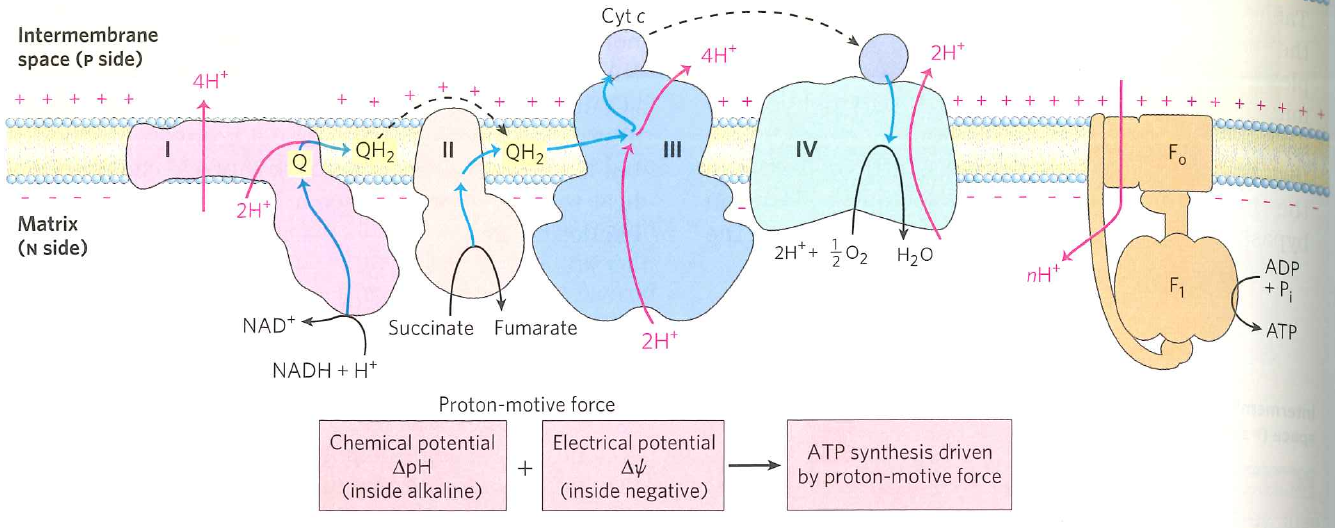
• What is the nature of the gradient? electro-chemical (proton motive force)
• What happens in the rotor ($F_{0}$)? proton transport is coupled to rotation
• What happens in subunit $F_{1}$? cooperative enzyme cycling catalyzes $ADP + P_{i} \rightarrow ATP$

How is energy stored in the $pH$ gradient between the matrix and the inter membrane space?

$\Delta G$ = concentration + electrical potential

$\Delta G = RTln \Big ( \frac{[H^{+}]_{out}}{[H^{+}]_{in}} \Big ) + ZF \Delta \psi$

Outline:

• What is the nature of the gradient? electro-chemical (proton motive force)
• What happens in the rotor ($F_{0}$)?
• What happens in subunit $F_{1}$?

The $F_{0}$ subunit consists of 10 identical subunits arranged in a circle

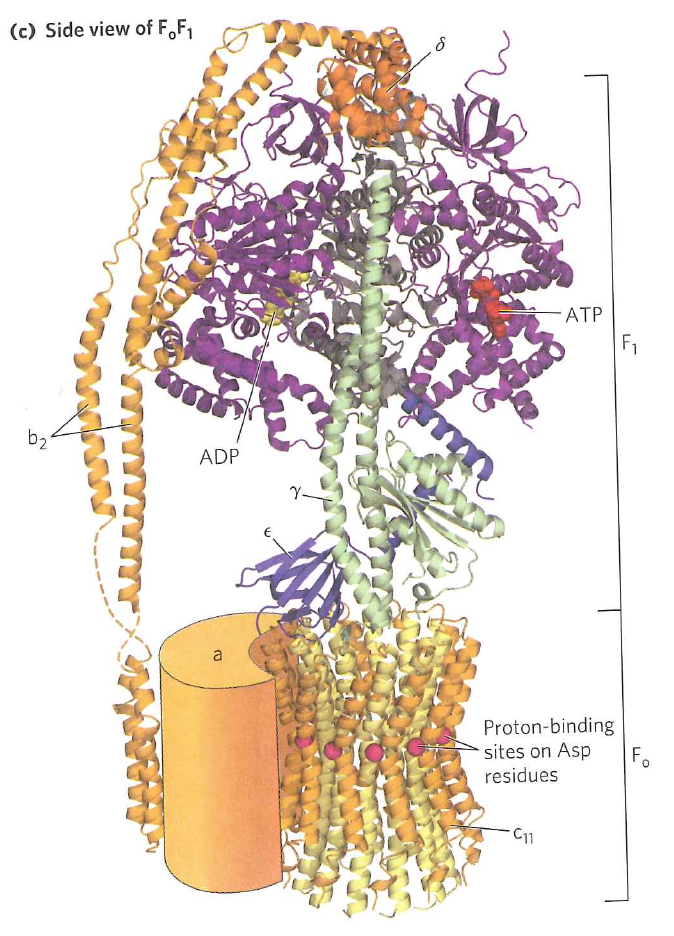
The $F_{0}$ subunit consists of 10 identical subunits arranged in a circle

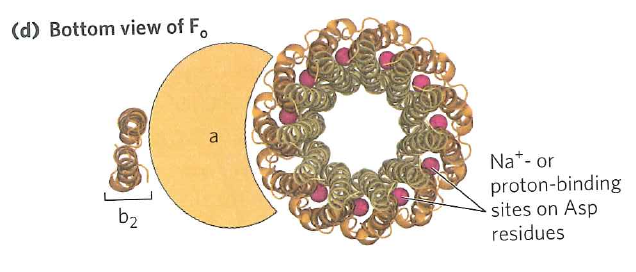
Which aspartic acid will be more protonated?

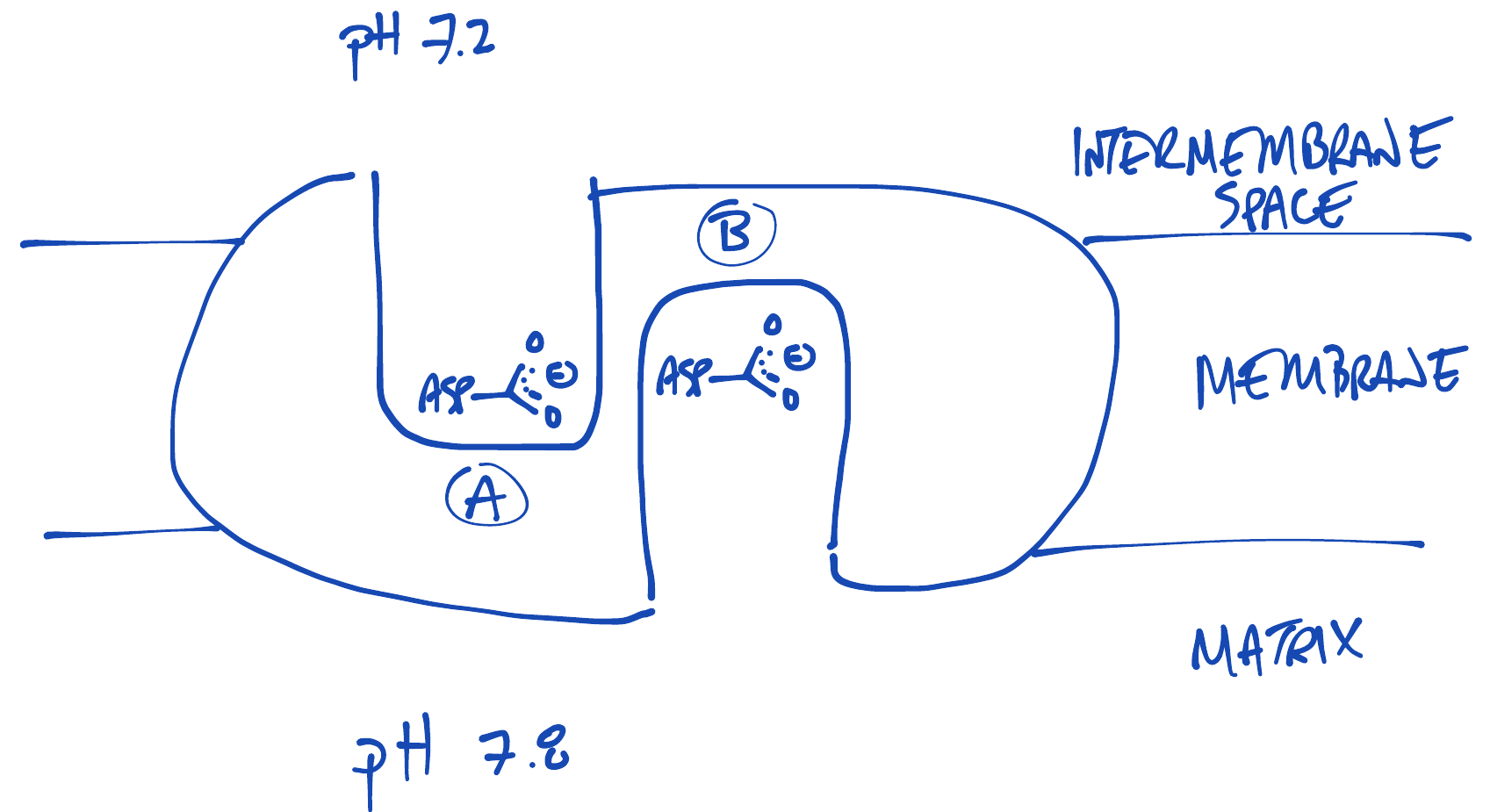
A

Would a protonated Asp or de-protonated Asp more easily cross a membrane bilayer?

Protonated. A protonated Asp is uncharged ($RCOOH$) while a deprotonated Asp is charged ($RCOO^{-} + H^{+}$)

Asp exposed to intermembrane space side protonates more than Asp exposed to matrix side

Protonated Asp enters bilayer more easily than deprotonated Asp

Brownian motion kicks protonated Asp "forward" more of than deprotonated Asp "backward"

Result is net forward motion

You can see this with a microscope. If you attach a flourescent actin polymer to ATPase, it spins

Outline:

• What is the nature of the gradient? electro-chemical (proton motive force)
• What happens in the rotor ($F_{0}$)? proton transport is coupled to rotation
• What happens in subunit $F_{1}$?

$F_{1}$ consists of three $\alpha \beta$ dimers

Each $\alpha \beta$ dimer can be in either $O$, $L$, or $T$ states (bizarre names just like $T$ and $S$ from hemoglobin).

System is cooperative. At all times, one subunit must be in $O$, one must be in $L$, one must be in $T$

Shaft connecting to $F_{0}$ ($\gamma$) is asymmetrical and stabilizes the $O$ state when bound

As $F_{0}$ spins, $\gamma$ pushes each subunit sequentially through $O \rightarrow L \rightarrow T$

How does this rotation lead to ATP synthesis?

$O$ has high affinity for $ADP$ and $P_{i}$ individually

$L$ brings $ADP$ and $P_{i}$ into close proximity

$T$ has high affinity for $ATP$. The $L \rightarrow T$ transition catalyzes formation of $ATP$

How do we get $ATP$ off?

$O$ state has low affinity for ATP

Each $120^{\circ}$ turn of $F_{0}$ pushes the $\alpha \beta$ dimers through one step of the cycle

This process yields (at max) $3 ATP$ per 10 protons

Electron transport moved 10 protons for 1 NADH

Max yield is thus 3 ATP per NADH.

With various inefficiencies, this is about ~2.5 ATP/NADH

Outline:

• What is the nature of the gradient? electro-chemical (proton motive force)
• What happens in the rotor ($F_{0}$)? proton transport is coupled to rotation
• What happens in subunit $F_{1}$? cooperative enzyme cycling catalyzes $ADP + P_{i} \rightarrow ATP$

• Energy is transduced from electro chemical to mechanical to chemical ($ATP$) in ATP synthase
• Despite mechanics being randomly driven by water slamming into system, the reaction goes forward
• This process yields ~2.5 ATP/NADH. It's very efficient.